题目内容
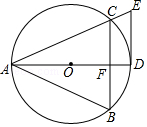
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
【答案】详见解析.
【解析】试题分析:(1)直接找一组勾股数代入方程即可;
(2)通过判断根的判别式△的正负来证明结论;
(3)利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
试题解析:
(1)解:令a=3,b=4则c=5,写出一个“勾系一元二次方程”:3x+5![]() x+4=0;
x+4=0;
(2)证明:
∵△=(![]() c)4ab=2c4ab=2(a+b)4ab=2(a2ab+b)=2(ab)≥0,
c)4ab=2c4ab=2(a+b)4ab=2(a2ab+b)=2(ab)≥0,
∴关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
(3)代入x=1得a![]() c+b=0,∴a+b=
c+b=0,∴a+b=![]() c.
c.
由四边形ACDE的周长是![]() 得a+b+a+b+
得a+b+a+b+![]() c=
c=![]() ,
,
∴2(a+b)+![]() c=
c=![]() ,2
,2![]() c+
c+![]() c=
c=![]() ,3
,3![]() c=
c=![]() ,c=2,a+b=2
,c=2,a+b=2![]() ,
,
∴2ab=(a+b)(a+b)=(a+b)(c)=84=4,
∴ab=2,
∴△ABC面积=![]()

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目