题目内容
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:
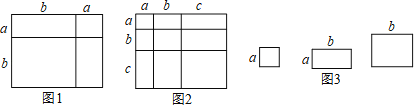
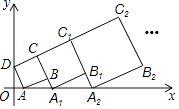
(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)见解析;(3)30;(4)156
【解析】分析:(1)直接求得正方形的面积,然后再根据正方形的面积=各矩形的面积之和求解即可;
(2)根据多项式的乘法法则计算出(a+b+c)2的结果,即可得到右边的式子;
(3)将a+b+c=10,ab+bc+ac=35代入(1)中得到的关系式,然后进行计算即可;
(4)长方形的面积xa2+yb2+zab =(5a+7b)(9a+4b),然后运算多项式乘多项式法则求得(5a+7b)(9a+4b)的结果,从而得到x、y、z的值.
详解:(1)∵正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc.
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)证明:(a+b+c)(a+b+c),
=a2+ab+ac+ab+b2+bc+ac+bc+c2=a2+b2+c2+2ab+2ac+2bc.
(3)a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,
=102﹣2(ab+ac+bc)=100﹣2×35=30.
(4)由题可知,所拼图形的面积为:xa2+yb2+zab,
∵(5a+7b)(9a+4b)=45a2+20ab+63ab+28b2=45a2+28b2+83ab,
∴x=45,y=28,z=83.∴x+y+z=45+28+83=156.