题目内容
【题目】一块三角形材料如图所示，∠A＝∠B＝60°，用这块材料剪出一个矩形DEFG，其中，点D，E分别在边AB，AC上，点F，G在边BC上．设DE＝x，矩形DEFG的面积s与x之间的函数解析式是s＝﹣
x2+
x，则AC的长是_____．
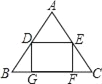
【答案】2．
【解析】
判断出△ABC是等边三角形，再根据等边三角形的性质可得BC=AC，然后表示出DE、GF之间的距离，再利用矩形的面积公式列式整理，然后根据AC的系数相等解答．
∵∠A=∠B=60°，
∴∠A=∠B=∠C，
∴△ABC是等边三角形，
∴BC=AC，
∵DE=x，
∴DE、GF之间的距离=
（BC-x）=（AC-x），
∴矩形DEFG的面积s=（AC-x）x=-x2+ACx，
又∵s与x之间的函数解析式是s=-x2+
x，
∴AC=2．
故答案为：2．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】（1）在下列表格中填上相应的值
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | -2 | 3 | 1 | … |
（2）若将上表中的变量
用y来代替（即有
），请以表中的
的值为点的坐标， 在下方的平面直角坐标系描出相应的点，并用平滑曲线顺次连接各点
（3）在（2）的条件下，可将y看作是x的函数 ，请你结合你所画的图像，写出该函数图像的两个性质 ：__________________________________________________.
（4）结合图像，借助之前所学的函数知识，直接写出不等式
的解集： ____________
