题目内容
【题目】给出下列命题及函数y=﹣x,y=﹣x2,y=![]() 的图象.①如果﹣a>﹣
的图象.①如果﹣a>﹣![]() >﹣a2,那么a<﹣1;②如果﹣
>﹣a2,那么a<﹣1;②如果﹣![]() >﹣a2>﹣a,那么﹣1<a<0;③如果﹣a2>﹣a>﹣
>﹣a2>﹣a,那么﹣1<a<0;③如果﹣a2>﹣a>﹣![]() ,那么0<a<1;④如果﹣
,那么0<a<1;④如果﹣![]() >﹣a2>﹣a.那么a>1,则正确命题的序号是( )
>﹣a2>﹣a.那么a>1,则正确命题的序号是( )
A. ①② B. ②③ C. ①③ D. ③④
【答案】C
【解析】
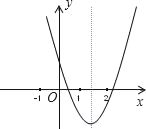
先画出函数y=-x,y=-x2,y=![]() 的图象,确定它们的交点坐标,然后观察图象的位置易得当-a>-
的图象,确定它们的交点坐标,然后观察图象的位置易得当-a>-![]() >-a2,则a<-1;当-a2>-a>-
>-a2,则a<-1;当-a2>-a>-![]() ,则0<a<1.
,则0<a<1.
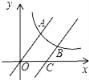
如图,

y=-x与y=-![]() 的交点坐标为(-1,1),(1,-1),函数y=-x与y=-x2的图象交点坐标为(0,0),(1,-1),函数y=-x2,y=
的交点坐标为(-1,1),(1,-1),函数y=-x与y=-x2的图象交点坐标为(0,0),(1,-1),函数y=-x2,y=![]() 的交点坐标为(1,-1);
的交点坐标为(1,-1);
当x<-1时,-x>-![]() >-x2,
>-x2,
当-1<x<0时,-![]() >-x>-x2,
>-x>-x2,
当0<x<1时,-x2>-x>-![]() ,
,
当x>1时,-![]() >-x>-x2,
>-x>-x2,
所以当-a>-![]() >-a2,则a<-1;当-a2>-a>-
>-a2,则a<-1;当-a2>-a>-![]() ,则0<a<1.
,则0<a<1.
故选C.

练习册系列答案
相关题目