题目内容
【题目】如图，在平面直角坐标系xOy中，直线l交x轴和y轴于点A，B，反比例函数y=
（x＞0）的图象于点C，过点C作y轴的平行线交x轴于点D，过点B作x轴的平行线交反比例函数y=-
（x＜0）的图象于点E，则图中阴影部分的总面积为______．
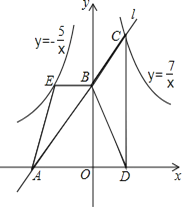
【答案】6
【解析】
连接OC、OE，由同底等高的三角形面积相等结合反比例函数系数k的几何意义，即可得出S△OBE=S△ABE=
×|-5|=2.5、S△OCD=S△BCD=×7=3.5，再将其代入S阴影=S△ABE+S△BCD中，即可求出阴影部分的总面积．
连接OC、OE，如图所示，
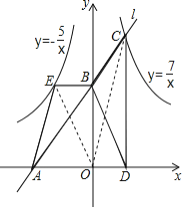
∵CD∥y轴，BE∥x轴，
∴S△OBE=S△ABE=×|-5|=2.5，
S△OCD=S△BCD=×7=3.5，
∴S阴影=△ABE+S△BCD=2.5+3.5=6，
故答案为：6．
练习册系列答案
相关题目
