题目内容
【题目】如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
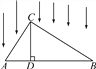
【答案】(1)AC的投影是AD,CD的投影是点D,BC的投影是BD;(2)证明见解析.
【解析】试题分析:(1)在平行投影中,投影线垂直于投影面产生的投影叫做正投影,根据正投影的定义求解即可;
(2)①,结合两角对应相等的两三角形相似,可得△BCD∽△BAC,根据相似三角形对应边成比例可证明结论;
②同理可证△ACD∽△CBD,根据相似三角形对应边成比例可证明结论成立.
试题解析:
解:(1)∵CD⊥AB,
而平行光线垂直AB,
∴AC的投影是AD,CD的投影是点D,BC的投影为BD;
(2)①∵∠ACB=90°,CD⊥AB于D,
∴∠ACB=∠CDB=90°.
∵∠B=∠B,
∴△BCD∽△BAC,
∴![]() ,
,
∴BC2=BDAB;
②同理可得:△ACD∽△CBD,
∴![]() ,
,
∴CD2=ADBD.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目