题目内容
抛物线y=n(n+1)x2-(3n+1)x+3与直线y=-nx+2的两个交点的横坐标分别是x1,x2,记dn=|x1-x2|.则代数式d1+d2+d3+…+d2010的值是分析:联立抛物线和直线的解析式,求得两个交点的横坐标,然后观察dn表达式的规律,根据规律进行求解即可.
解答:解:依题意,联立抛物线和直线的解析式有:
n(n+1)x2-(3n+1)x+3=-nx+2,
整理得:n(n+1)x2-(2n+1)x+1=0,
解得x1=
,x2=
;
所以当n为正整数时,dn=
-
,
故代数式d1+d2+d3+…+d2010=1-
+
-
+…+
-
=1-
=
.
n(n+1)x2-(3n+1)x+3=-nx+2,
整理得:n(n+1)x2-(2n+1)x+1=0,
解得x1=
| 1 |
| n |
| 1 |
| n+1 |
所以当n为正整数时,dn=
| 1 |
| n |
| 1 |
| n+1 |
故代数式d1+d2+d3+…+d2010=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2011 |
| 1 |
| 2011 |
| 2010 |
| 2011 |
点评:此题主要考查的是函数图象交点坐标的求法,能够发现所求代数式中的规律是解决问题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 A和C,和x轴的另一个交点为B.
A和C,和x轴的另一个交点为B.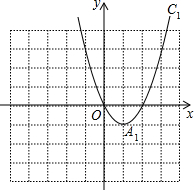 已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.
已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.