题目内容
抛物线y=(k2-2)x2-4kx+m的对称轴是直线x=2,且它的最低点在直线y=-2x+2上,求:(1)函数解析式;
(2)若抛物线与x轴交点为A、B与y轴交点为C,求△ABC面积.
分析:(1)先根据对称轴公式求出k的值,再利用直线y=-2x+2求出抛物线的顶点坐标,代入二次函数解析式即可求出m的值,从而完整的求出了函数解析式.
(2)先由(1)中所求的解析式求出抛物线分别与x,y轴的交点坐标,确定A、B、C的位置再根据三角形的面积公式求解.
(2)先由(1)中所求的解析式求出抛物线分别与x,y轴的交点坐标,确定A、B、C的位置再根据三角形的面积公式求解.
解答:解:(1)∵抛物线y=(k2-2)x2-4kx+m的对称轴是直线x=2
∴
=2
解得k=-1或k=2
又∵图象有最低点,即开口向上
∴k2-2>0,即k2>2
∴k=2
即y=2x2-8x+m
把x=2代入直线y=-2x+2得
y=-2
即抛物线的顶点坐标是(2,-2)
代入函数y=2x2-8x+m得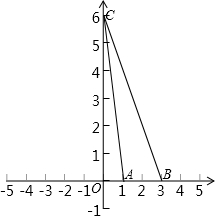
m=6
∴函数解析式为y=2x2-8x+6;
(2)当x=0时,y=6,即点C的坐标是(0,6)
当y=0时,2x2-8x+6=0,解得x=1或x=3,
即点A、B的坐标分别是(1,0)、(3,0)
则AB=3-1=2,OC=6
∴S△ABC=
AB•OC=
×2×6=6.
∴
| 4k |
| 2(k2-2) |
解得k=-1或k=2
又∵图象有最低点,即开口向上
∴k2-2>0,即k2>2
∴k=2
即y=2x2-8x+m
把x=2代入直线y=-2x+2得
y=-2
即抛物线的顶点坐标是(2,-2)
代入函数y=2x2-8x+m得

m=6
∴函数解析式为y=2x2-8x+6;
(2)当x=0时,y=6,即点C的坐标是(0,6)
当y=0时,2x2-8x+6=0,解得x=1或x=3,
即点A、B的坐标分别是(1,0)、(3,0)
则AB=3-1=2,OC=6
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:主要考查了二次函数解析式的求法.本题主要是根据对称轴公式和点在直线上的意义求出二次函数解析式中未知数的值,从而求出解析式.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目