题目内容
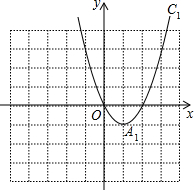 已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.
已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.(1)求抛物线C1的顶点A坐标,并画出抛物线C2的图象;
(2)若直线y=kx+b与抛物线y=ax2+bx+c(a≠0)有且只有一个交点时,称直线与抛物线相切.若直线y=x+b与抛物线C1相切,求b的值;
(3)结合图象回答,当直线y=x+b与图象C3有两个交点时,b的取值范围.
分析:(1)用配方法将C1化为顶点坐标式,即可得到它的顶点坐标;由于C2、C1关于y轴对称,那么C2、C1的开口方向和开口大小都相同,而它们的顶点坐标也关于y轴对称,可据此画出C2的图象.
(2)联立直线y=x+b和抛物线C1的解析式,消去y后可得到关于x的一元二次方程,若两函数图象只有一个交点,那么方程的判别式△=0,由此求得b的值①.
(3)可参照(2)的解法求出当直线y=x+b与C2相切时b的值②,若此直线与C3有两个交点,那么b的取值范围必在①②的范围之内,由此得解.
(2)联立直线y=x+b和抛物线C1的解析式,消去y后可得到关于x的一元二次方程,若两函数图象只有一个交点,那么方程的判别式△=0,由此求得b的值①.
(3)可参照(2)的解法求出当直线y=x+b与C2相切时b的值②,若此直线与C3有两个交点,那么b的取值范围必在①②的范围之内,由此得解.
解答:解:(1)∵抛物线C1:y=x2-2x=(x-1)2-1;
∴顶点坐标A(1,-1).(1分)
图如右图;(2分)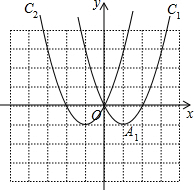
(2)
把(1)式代入(2)
整理得:x2-3x-b=0;
△=9+4b=0,b=-
.(4分)
(3)∵C1的图象沿y轴翻折,得到抛物线C2的图象,
∴由题意可得出:抛物线C2:y=x2+2x,
∴
把(1)式代入(2)
整理得:x2+x-b=0;
△=1+4b=0,b=-
.(6分)
∴当直线y=x+b与图象C3有两个交点时,b的取值范围为:-
<b<-
.(7分)
∴顶点坐标A(1,-1).(1分)
图如右图;(2分)

(2)
|
把(1)式代入(2)
整理得:x2-3x-b=0;
△=9+4b=0,b=-
| 9 |
| 4 |
(3)∵C1的图象沿y轴翻折,得到抛物线C2的图象,
∴由题意可得出:抛物线C2:y=x2+2x,
∴
|
把(1)式代入(2)
整理得:x2+x-b=0;
△=1+4b=0,b=-
| 1 |
| 4 |
∴当直线y=x+b与图象C3有两个交点时,b的取值范围为:-
| 9 |
| 4 |
| 1 |
| 4 |
点评:此题主要考查函数图象的几何变换、函数图象交点坐标的求法、根的判别式等知识,难度适中.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
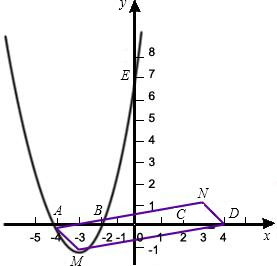 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).