题目内容
如图,直线y=| 4 |
| 3 |
| 4 |
| 3 |
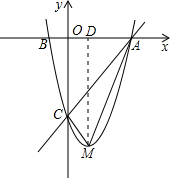
 A和C,和x轴的另一个交点为B.
A和C,和x轴的另一个交点为B.(1)求该二次函数的关系式;
(2)直接写出该抛物线的对称轴及顶点M的坐标;
(3)求四边形ABCM的面积S.
分析:(1)由直线y=
x-4与x轴交于点A,与y轴交于点C,分别令x=0与y=0,即可求得点A和C的坐标,又由二次函数y=
x2+bx+c的图象经过点A和C,利用待定系数法即可求得此二次函数的关系式;
(2)由(1)中的二次函数的关系式,利用配方法即可求得其顶点式,则可求得该抛物线的对称轴及顶点M的坐标.
(3)首先令y=
x2-
x-4中,y=0,得方程
x2-
x-4=0,解此方程即可求得点B的坐标,然后过M作x轴的垂线,垂足为D,由S四边形ABCM=S△OBC+S梯形OCDM+S△ADM,即可求得四边形ABCM的面积S的值.
| 4 |
| 3 |
| 4 |
| 3 |
(2)由(1)中的二次函数的关系式,利用配方法即可求得其顶点式,则可求得该抛物线的对称轴及顶点M的坐标.
(3)首先令y=
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
解答:解:(1)∵直线y=
x-4与x轴交于点A,与y轴交于点C,
∴当x=0时,y=-4,当y=0时,x=3,
∴A(3,0),C(0,-4),
∵二次函数y=
x2+bx+c的图象经过点A和C,
∴
,
解得:
,
∴该二次函数的关系式为:y=
x2-
x-4;
(2)∵y=
x2-
x-4=
(x2-2x)-4=
(x-1)2-
,
∴该抛物线的对称轴为x=1,顶点M的坐标为(1,-
).
(3)令y=
x2-
x-4中,y=0,得
x2-
x-4=0,
∴x2-2x-3=0,
解得:x1=-1,x2=3,
∴B(-1,0),
过M作x轴的垂线,垂足为D,
S四边形ABCM=S△OBC+S梯形OCDM+S△ADM=
×1×4+
×(4+
)×1+
×(3-1)×
=12.
| 4 |
| 3 |
∴当x=0时,y=-4,当y=0时,x=3,
∴A(3,0),C(0,-4),
∵二次函数y=
| 4 |
| 3 |
∴
|
解得:
|
∴该二次函数的关系式为:y=
| 4 |
| 3 |
| 8 |
| 3 |
(2)∵y=
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
∴该抛物线的对称轴为x=1,顶点M的坐标为(1,-
| 16 |
| 3 |

(3)令y=
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
∴x2-2x-3=0,
解得:x1=-1,x2=3,
∴B(-1,0),
过M作x轴的垂线,垂足为D,
S四边形ABCM=S△OBC+S梯形OCDM+S△ADM=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
点评:此题考查了二次函数与一次函数的综合应用.此题综合性较强,难度较大,解题的关键是注意待定系数法求函数解析式,注意二次函数的一般式与顶点式的转化,注意在求四边形的面积时辅助线的作法与分割思想的应用.

练习册系列答案
相关题目
 在,请说明理由;
在,请说明理由;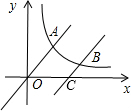 如图,直线y=
如图,直线y=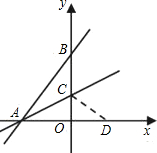 如图,直线y=
如图,直线y=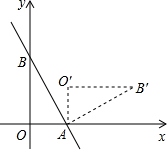 如图,直线y=-
如图,直线y=-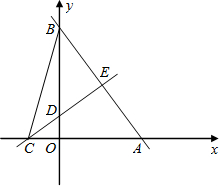 (2012•营口)如图,直线
(2012•营口)如图,直线