Question

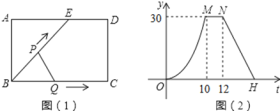
【题目】如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是，设P，Q出发t秒时，的面积为，已知y与t的函数关系的图象如图曲线OM为抛物线的一部分，则下列结论：；直线NH的解析式为；不可能与相似；当时，秒．其中正确的结论个数是（ ）

A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

据图(2)可以判断三角形的面积变化分为三段，可以判断出当点P到达点E时点Q到达点C，从而得到BC、BE的长度，即可判断①，再根据M、N是从10秒到12秒，可得ED的长度，, 当点P运动到点C时，面积变为0，可求得点H的坐标，求出解析式，即可判断②，当△ABE与△QBP相似时，点P在DC上，求出PQ的长，即可判断③，t=13时，PQ=5,此时tan∠PBQ==，即可判断④．

解：①据图(2)可得，当点P到达点E时点Q到达点C，
∵点P、Q的运动的速度都是1cm/s，
∴BC=BE=10cm，S△BCE= BC·AB=30,
∴AB=6,故①正确；

②根据1012秒面积不变，可得ED=2，
当点P运动到点C时，面积变为0，此时点P走过的路程为BE+ED+DC=18，
故点H的坐标为(18,0)，
设直线NH的解析式为y=kx+b，
将点H(18,0)，点N(12,30)代入可得：，
解得：．
故直线NH的解析式为：y=5t+90，故②正确；
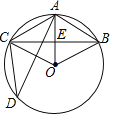
③当△ABE与△QBP相似时，点P在DC上，如图2所示：

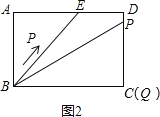
∵tan∠PBQ=tan∠ABE=，
∴，

∵BQ=10，

∴PQ=7.5,

∴PQ＞CD,

∴△ABE与△QBP不可能相似，故③正确；

④t=13时，PQ=18-13=5,

此时tan∠PBQ==,

∴∠PBQ≠30,故④错误，

综上可得①②③正确，共3个．
故选C．