题目内容
【题目】如图，在矩形ABCD中，E，F分别是AD，BC的中点，AF与BE相交于点M，CE与DF相交于点N，QM⊥BE，QN⊥EC相交于点Q，PM⊥AF，PN⊥DF相交于点P，若2BC=3AB，记△ABM和△CDN的面积和为S，则四边形MQNP的面积为（ ）
A. 
S B. 
S C. 
S D. 
S
【答案】C
【解析】
连接EF．证明
≌
，设
，则
连接MN交EF于O，则
证明
根据相似三角形的性质得到
进而求出S菱形MQNP
即可求出四边形MQNP的面积
连接EF．
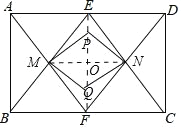
∵四边形ABCD是矩形，
∴四边形ABFE，四边形CDEF都是矩形，且是全等的矩形，
∴
∵
∴
连接PF，在和 中，
∴≌，
∴
∴E、P、F共线，同法可证，E、Q、F共线，则易证四边形MQNP是菱形，
∵
，
设，则连接MN交EF于O，则
∵
∴
∴
∴S菱形MQNP
∵
和
的面积和为S，
∴
∴
∴S菱形MQNP
故选：C．
练习册系列答案
相关题目
