题目内容
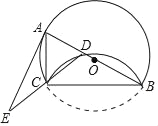
【题目】如图,以AB为直径作⊙O,点C为⊙O上一点,劣弧CB沿BC翻折,交AB于点D,过A作⊙O的切线交DC的延长线于点E.
(1)求证:AC=CD;
(2)已知tanE=![]() ,AC=2,求⊙O的半径.
,AC=2,求⊙O的半径.
【答案】(1)证明见解析;(2)⊙O的半径为![]() .
.
【解析】
(1)根据折叠的性质与圆周角定理即可得证;
(2)根据切线的性质与圆周角定理易证∠E=∠ABC,则在Rt△ABC利用三角形函数与勾股定理求得AB=2![]() ,即⊙O的半径为
,即⊙O的半径为![]() .
.
(1)如图所示:
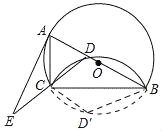
∵点D与点D′关于CB对称,
∴CD=CD′,∠DBC=∠D′BC,
∴AC=CD′,
∴AC=CD;
(2)∵AE为⊙O的切线,
∴∠BAE=90°,
∴∠E+∠ADC=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵AC=CD,
∴∠CAB=∠ADC,
∴∠E=∠ABC,
∴tanE=tan∠ABC=![]() =
=![]() ,
,
∵AC=2,
∴BC=4,
则AB=![]() ,
,
∴⊙O的半径为![]() .
.

练习册系列答案
相关题目