题目内容
【题目】如图所示,正三角形ABC的边长为3+![]() .
.
(1)如图,正方形EFPN的顶点E,F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的面积.

【答案】(1)见解析;(2) 36-18![]() .
.
【解析】
(1)利用位似图形的性质,作出正方形EFPN的位似正方形E′F′P′N′,如图所示;
(2)根据正三角形、正方形、直角三角形相关线段之间的关系,利用等式E′F′+AE′+BF′=AB,列方程求得正方形E′F′P′N′的边长,即可求解.
(1)如图,正方形E′F′P′N′即为所求.
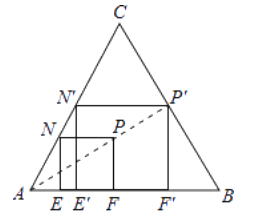
(2)设正方形E′F′P′N′的边长为x,
∵△ABC为正三角形,
∴AE′=BF′=![]() x.
x.
∵E′F′+AE′+BF′=AB,
∴x+![]() x+
x+![]() x=3+
x=3+![]() ,
,
∴x=![]() ,即x=3
,即x=3![]() -3.
-3.
故(1)中作出的正方形E′F′P′N′的边长3![]() -3,
-3,
则E′F′P′N′的面积为:(3![]() -3)= 36-18
-3)= 36-18![]() .
.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目