题目内容
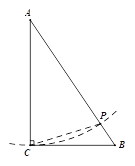
【题目】如图,△ABC中,∠C=90°,BC=5.
⑴ 利用直尺和圆规在AB边上求作一点P,使得∠APC+∠BCP=90°,并说明理由;(不写作法,保留作图痕迹)
⑵ 在⑴的条件下,试判断∠PCB与∠A之间的数量关系,并说明理由.

【答案】(1)见解析;(2)∠A=2∠PCB ,理由见解析.
【解析】
(1)在AB上截取AP=AC,利用等腰三角形的性质可证点P为所求作的点
(2)利用等腰三角形的两个底角相等,求出![]() ,化简可得
,化简可得
![]() ,利用∠ACB=90°,可证
,利用∠ACB=90°,可证![]() ,即:∠A=2∠PCB.
,即:∠A=2∠PCB.
⑴ 如图,在AB上截取AP=AC,则点P为所求作的点
∵ AP=AC
∴ ∠ACP=∠APC
∵ ∠ACB=90° ∴ ∠ACP+∠PCB=90°
∴ ∠APC+∠PCB=90°
⑵ 判断:∠A=2∠PCB
∵ AC=AP
∴![]() 即:
即:![]() ,
,
∵ ∠ACB=90°
∴ ∠ACP+∠PCB=90° 即:∠PCB=90°-∠ACP
∴ ![]()
即:∠A=2∠PCB

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目