题目内容
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF , 其中正确的是( ) 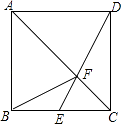
A.①③
B.②③
C.①④
D.②④
【答案】C
【解析】解:∵四边形ABCD是正方形, ∴AD∥CB,AD=BC=AB,∠FAD=∠FAB,
在△AFD和△AFB中,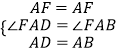 ,
,
∴△AFD≌△AFB,
∴S△ABF=S△ADF , 故①正确,
∵BE=EC= ![]() BC=
BC= ![]() AD,AD∥EC,
AD,AD∥EC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴S△CDF=2S△CEF , S△ADF=4S△CEF , S△ADF=2S△CDF ,
故②③错误④正确,
故选C.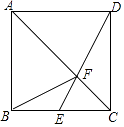
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目