Question

【题目】如图，A、B、C三点在数轴上，A表示的数为-10，B表示的数为14，点C为线段AB的中点，动点P在数轴上，且点P表示的数为m．

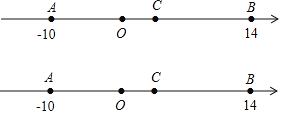
(1)求点C表示的数；

(2)点P从A点出发，沿射线AB向终点B运动，设BP的中点为M，用含m的整式表示线段MC的长．

(3)在(2)的条件下，当m为何值时，AP-CM=2PC．

Answer 1

【答案】(1)点C表示的数为2；(2)MC= 5+m；(3)m=6或m=-．

【解析】

（1）根据线段的中点坐标公式即可求出点C表示的数；

（2）根据线段中点的定义可得再代入MC=BC-BM，计算即可求解；

（3）用含m的代数式分别表示AP=m+10，，PC=|m-2|，代入AP-CM=2PC，解方程即可．

(1)∵A表示的数为-10，B表示的数为14，点C为线段AB的中点，

∴点C表示的数为=2；

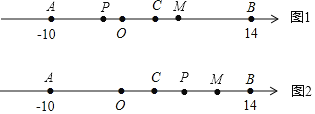
(2)∵BP的中点为M，

∴BM=BP=(14-m)，

∴MC=BC-BM=12-(14-m)=5+m；

(3)∵AP=m+10，CM=5+m，PC=|m-2|，

∴当AP-CM=2PC时，m+10-(5+m)=2|m-2|，

∴m+5=2m-4，或m+5=-(2m-4)，

解得m=6，或m=-．