��Ŀ����
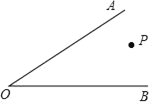
����Ŀ����ͼ���������ϵ�A��ʾ��������Ϊ![]() ����B��ʾ��������Ϊ6����P�ӵ�A������ÿ��2����λ���ȵ��ٶ���
����B��ʾ��������Ϊ6����P�ӵ�A������ÿ��2����λ���ȵ��ٶ���![]() �˶���ͬʱ����Q�ӵ�B������ÿ��1����λ���ȵ��ٶ���
�˶���ͬʱ����Q�ӵ�B������ÿ��1����λ���ȵ��ٶ���![]() �˶�������Q�����AʱP��Q����ֹͣ�˶������˶�ʱ��Ϊ
�˶�������Q�����AʱP��Q����ֹͣ�˶������˶�ʱ��Ϊ![]() ��λ����
�����![]() ��
��
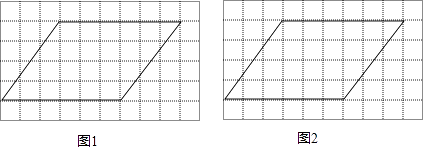
��1����![]() ʱ�����P�͵�Q��ʾ����������
ʱ�����P�͵�Q��ʾ����������
��2�����P���Q��һ���غ�ʱ��tֵ��
��3����t��ֵΪ����ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�
![]()
���𰸡�![]() ��P��ʾ����Ϊ
��P��ʾ����Ϊ![]() ����Q��ʾ����Ϊ
����Q��ʾ����Ϊ![]() ��
��![]() ��P���Q��һ���غ�ʱ��tֵΪ4��
��P���Q��һ���غ�ʱ��tֵΪ4��![]() ��t��ֵΪ3��5��9ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�
��t��ֵΪ3��5��9ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�
��������
![]() ����������Եõ���
����������Եõ���![]() ʱ����P�͵�Q��ʾ����������
ʱ����P�͵�Q��ʾ����������
![]() ������������г���������t�ķ��̣��Ӷ��������t��ֵ��
������������г���������t�ķ��̣��Ӷ��������t��ֵ��
![]() ������������г���Ӧ�ķ��̣��Ӷ����Խ���⣮
������������г���Ӧ�ķ��̣��Ӷ����Խ���⣮
![]() ��
��![]() ʱ��
ʱ��
��P��ʾ����Ϊ��![]() ��
��
��Q��ʾ����Ϊ��![]() ��
��
![]()
![]()
![]()
![]() ��
��
�𣺵�P���Q��һ���غ�ʱ��tֵΪ4��
![]() ��P�͵�Q��һ����ǰ��
��P�͵�Q��һ����ǰ��
![]() ��
��
��ã�![]() ��
��
����P�͵�Q������P�����Bǰ��
![]() ��
��
��ã�![]() ��
��
����P�ӵ�B���A�˶�ʱ��
![]() ��
��
��ã�![]() ��
��
���Ͽɵã���t��ֵΪ3��5��9ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�