题目内容
【题目】有两个函数
和
，若对于每个使函数有意义的实数
，函数
的值为两个函数值中的较小的数，则称函数为这两个函数
的较小值函数．例如：
，则的较小值函数为
（1）函数是函数
的较小值函数．
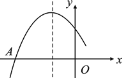
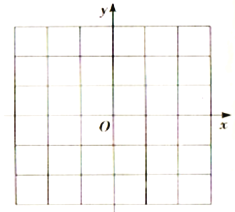
①在如图的平面直角坐标系中两出函数的图象．
②求函数的图象与轴的交点坐标．
（2）函数是函数
的较小值函数．
①写出函数的两条性质．
②当
时，函数值的取值范围为
．当
取某个范围内的任意值时，
为定值，直接写出满足条件的的取值范围及其对应的的值．
【答案】（1）①见解析；②函数y的图象与x轴的交点坐标为（-2，0）、（1，0）；（2）①性质：函数图象位于一、三象限；当x≤-1或0＜x≤1时，y随x的增大而增大；②
≤a≤1，b=1
【解析】
（1）①根据较小值函数的定义结合y1，y2的解析式作图即可；
②当y=0时，由x+2=0和-2x+2=0可求得交点坐标；
（2）①画出y的大致图象，根据图象写出两条性质即可；
②求出y=时，
或，然后根据题意结合函数图象可得
的值以及
的取值范围.
解：（1）①如图所示：
②当y=0时，由x+2=0得x=-2，由-2x+2=0得x=1，
∴函数y的图象与x轴的交点坐标为（-2，0）、（1，0）；
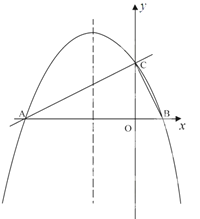
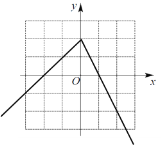
（2）函数y的大致图象如图所示：
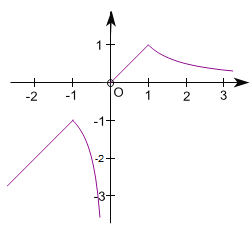
①性质：函数图象位于一、三象限；②当x≤-1或0＜x≤1时，y随x的增大而增大；
②当y=时，即
或
，
∴或，
∵当
时，函数值
的取值范围为
，且当取某个范围内的任意值时，为定值，
∴根据函数图象的最大值为1可知，b=1，
∵y取最大值时x=1，
∴a的取值范围为：≤a≤1．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】为了丰富同学们的知识，拓展阅读视野，学习图书馆购买了一些科技、文学、历史等书籍，进行组合搭配成
、
、
三种套型书籍，发放给各班级的图书角供同学们阅读，已知各套型的规格与价格如下表：
|
|
| |
规格（本/套） | 12 | 9 | 7 |
价格（元/套） | 200 | 150 | 120 |
（1）已知搭配、两种套型书籍共15套，需购买书籍的花费是2120元，问、两种套型各多少套？
（2）若图书馆用来搭配的书籍共有2100本，现将其搭配成、两种套型书籍，这两种套型的总价为30750元，求搭配后剩余多少本书？
（3）若图书馆用来搭配的书籍共有122本，现将其搭配成、、三种套型书籍共13套，且没有剩余，请求出所有搭配的方案．
