Question

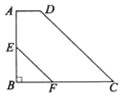
【题目】如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，CF⊥AF，且CF=CE．

（1）求证：CF是⊙O的切线；

（2）若sin∠BAC=，求的值．

Answer 1

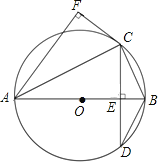
【答案】（1）证明：连接OC．

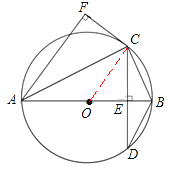
∵CE⊥AB，CF⊥AF，CE=CF，

∴AC平分∠BAF，即∠BAF=2∠BAC。

∵∠BOC=2∠BAC，∴∠BOC=∠BAF。

∴OC∥AF。∴CF⊥OC。∴CF是⊙O的切线。

（2）解：∵AB是⊙O的直径，CD⊥AB，

∴CE=ED，∠ACB=∠BEC=90°。

∴S△CBD=2S△CEB，∠BAC=∠BCE。∴△ABC∽△CBE。

∴。∴。

【解析】

（1）首先连接OC，由CD⊥AB，CF⊥AF，CF=CE，即可判定AC平分∠BAF，由圆周角定理即可得∠BOC=2∠BAC，则可证得∠BOC=∠BAF，即可判定OC∥AF，即可证得CF是⊙O的切线。

（2）由垂径定理可得CE=DE，即可得S△CBD=2S△CEB，由△ABC∽△CBE，根据相似三角形的面积比等于相似比的平方，易求得△CBE与△ABC的面积比，从而可求得的值。