Question

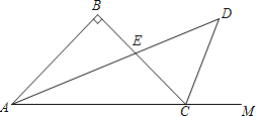
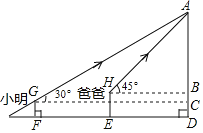
【题目】乐山独峰，倚天独立．身高1.6米的小明（GF）和身高1.8米的爸爸（HE）前去游览，山腰处的一棵缀满红叶的枫树（A）吸引了他们的目光，已知小明的仰角为30°，爸爸的仰角为45°，若小明与爸爸之间（EF）相距6米，求枫树（A）与地面的距离（AD）为多少米？（参考数据：1.41，1.73，结果保留一位小数．）

Answer 1

【答案】枫树（A）与地面的距离（AD）为9.3米

【解析】

过H作HB⊥AD于B，作GC⊥AD于C，解直角三角形即可得到结论．

解：过H作HB⊥AD于B，作GC⊥AD于C，

在Rt△AHB中，∠AHB＝45°，∠ABH＝90°，

∴AB＝BH＝a，

∵BC＝HE﹣GF＝1.8﹣1.6＝0.2m，

∴AC＝a+0.2，

在Rt△AGC中，tan30°＝，

∴＝，

解得：a≈7.70，

∴AD＝7.70+1.6＝9.3（米），

答：枫树（A）与地面的距离（AD）为9.3米