题目内容
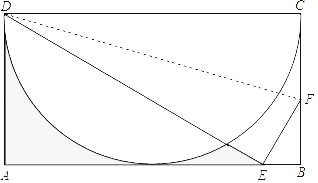
【题目】如图所示,ABCD为矩形,以CD为直径作半圆,矩形的另外三边分别与半圆相切,沿着折痕DF折叠该矩形,使得点C的对应点E落在AB边上,若AD=2,则图中阴影部分的面积为_____.
【答案】![]()
【解析】
作OH⊥AB于H,DE交半圆于M,连接OM,作ON⊥DM于N,如图,利用切线的性质得CD=2OH=4,再根据折叠的性质得DE=DC=4,则根据正弦的定义得到∠AED=30°,AE=![]() ,AD=2
,AD=2![]() ,接着求出∠DOM=120°,然后根据三角形面积公式、扇形的面积公式,利用图中阴影部分的面积=S△ADE﹣S弓形DHM=S△ADE﹣(S扇形DOM﹣S△DOM)进行计算.
,接着求出∠DOM=120°,然后根据三角形面积公式、扇形的面积公式,利用图中阴影部分的面积=S△ADE﹣S弓形DHM=S△ADE﹣(S扇形DOM﹣S△DOM)进行计算.
解:作OH⊥AB于H,DE交半圆于M,连接OM,作ON⊥DM于N,如图,
∵矩形的另外三边分别与半圆相切,
∴OH为半圆的半径,
∴CD=2OH=2AD=4,
∵DC沿DF折叠到DE,
∴DE=DC=4,
在Rt△ADE中,∵sin∠AED=![]() ,
,
∴∠AED=30°,
∴AE=![]() ,AD=2
,AD=2![]() ,
,
∵CD∥AB,
∴∠CDE=∠AEB=30°,
∵OD=OM,
∴∠ODM=∠OMD=30°,
∴∠DOM=120°,
∴图中阴影部分的面积=S△ADE﹣S弓形DHM=S△ADE﹣(S扇形DOM﹣S△DOM)=![]() .
.
故答案为![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目