题目内容
【题目】如图,在正方形ABCD中,E为CD上一动点,(点E不与C、D重合)且CD=nDE, F为AD上一动点,且AE⊥FG于点H.
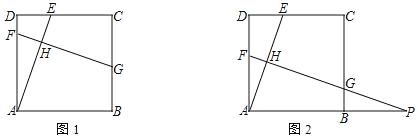
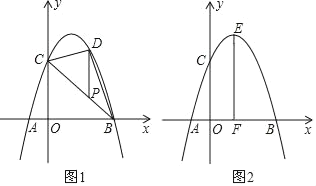
(1)如图1,求证:AE=FG;
(2)延长FG、AB相交于点P,且AH=EH;
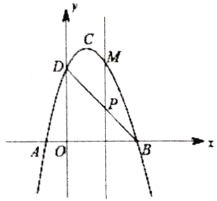
①n=3,求证:FH+PG=HG;
②若G是PH的中点,直接写出n的值.
【答案】(1)证明见解析;
(2)①证明见解析;②![]() 或
或![]() .
.
【解析】
(1)如图1中,作GK⊥AD于K.证明△ADE≌△GKF(ASA)即可解决问题.
(2)①如图2中,设FH=a.由tan∠DAE=tan∠P,推出![]() ,可得AH=EH=3a,PH=9a,求出HG,PG即可证明.
,可得AH=EH=3a,PH=9a,求出HG,PG即可证明.
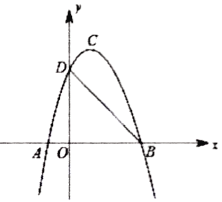
②如图2中,设AH=EH=x,FH=y,GH=PG=m.构建方程组,求出x,y(用m表示),即可解决问题.
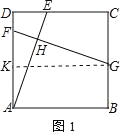
(1)证明:如图1中,作GK⊥AD于K.
∵四边形ABCD是正方形,
∴∠DAB=∠B=∠GKA=90°,
∴四边形ABGK是矩形,
∴AB=GK=AD,
∵FG⊥AE,
∴∠AHF=90°,
∵∠DAE+∠AFH=90°,∠AFH+∠FGK=90°,
∴∠DAE=∠KGF,
∵∠D=∠GKF=90°,
∴△ADE≌△GKF(ASA),
∴AE=FG.
(2)①证明:如图2中,设FH=a.
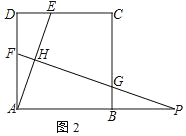
∵CD=nDE,n=3,
∴CD=3DE,
∵四边形ABCD是正方形,
∴∠D=∠DAB=90°,CD=AD,
∵∠AHF=90°,
∴∠DAE+∠PAH=90°,∠PAH+∠P=90°,
∴∠DAE=∠P,
∴tan∠DAE=tan∠P,
∴![]() ,
,
∴AH=EH=3a,PH=9a,
∵AE=FG=6a,
∴HG=5a,PG=4a,
∴FH+PG=5a,
∴FH+PG=HG.
②如图2中,设AH=EH=x,FH=y,GH=PG=m.
∵AE=FG,
∴2x=y+m,
∵△AHF∽△PHA,
∴AH2=FHPH,
∴x2=y2m,
∴x2﹣4xm+2m2=0,
解得![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
∴![]()
∴![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案