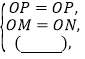Question

【题目】在△ABC中，AB=BC，∠ABC=90°．以AB为斜边作等腰直角三角形ADB．点P是直线DB上一个动点，连接AP，作PE⊥AP交BC所在的直线于点E．

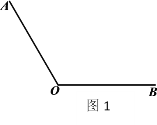
（1）如图1，点P在BD的延长线上，PE⊥EC，AD=1，直接写出PE的长；

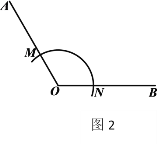
（2）点P在线段BD上（不与B，D重合），依题意，将图2补全，求证：PA=PE；

（3）点P在DB的延长线上，依题意，将图3补全，并判断PA=PE是否仍然成立．

Answer 1

【答案】(1)； (2)证明见解析；（3）证明见解析.

【解析】

（1）根据等腰直角三角形的性质得到∠ABP=45°，根据勾股定理得到AB==，推出四边形ABEP是矩形，得到四边形ABEP是正方形，于是得到结论；（2）根据等腰直角三角形的性质得到∠ADB=90°，∠DAB=∠DBA=45°，求得∠PBN=45°过P作PM⊥AB于点M，过P作PN⊥BC于点N，于是得到PM=PN，∠BPN=45°根据全等三角形的性质即可得到结论；

（3）根据等腰直角三角形的性质得到∠ABD=45°，得到∠PBN=45°，∠ABC=90°，过P作PM⊥AB于点M，过P作PN⊥BC于点N，得到四边形BMPN是矩形，推出四边形BMPN是正方形，得到PM=PN，根据全等三角形的性质即可得到结论．

（1）∵AD=DB=1，∠ADB=90°，

∴∠ABP=45°，AB==，

∵PE⊥AP，AB⊥BC，

∴PA∥EC，

∴PA⊥AB，

∴四边形ABEP是矩形，

∵∠ABP=45°，

∴PA=AB，

∴四边形ABEP是正方形，

∴PE=AB=

（2）∵△ABC和△ADB是等腰直角三角形，

∴∠ADB=90°，∠DAB=∠DBA=45°，

∴∠PBN=45°

∴PE⊥AP，∠DAP=∠BPE=90°-∠DPA，

∵∠PAM=45°-∠DAP，∠PEN=45°-∠BPE，

∴∠PAM=∠PEN，

过P作PM⊥AB于点M，过P作PN⊥BC于点N，

则PM=PN，∠BPN=45°，

在△APM和△EPN中，

，

∴△APM≌△EPN，

∴PA=PE；

（3）∵△ABC和△ADB是等腰直角三角形，

∴∠ABD=45°，

∴∠PBN=45°，∠ABC=90°，

过P作PM⊥AB于点M，过P作PN⊥BC于点N，

则四边形BMPN是矩形，

∵∠NBP=45°，

∴四边形BMPN是正方形，

∴PM=PN，

∵AB⊥BC，

∴∠BAN=∠APN，

∵AP⊥PE，

∴∠APN=∠E，

∴∠BAP=∠E，

在△AMP与△ENP中，

，

∴△AMP≌△ENP，

∴AP=PE．