题目内容
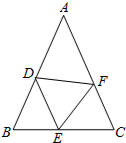
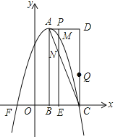
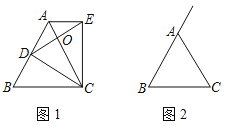
【题目】如图1,在等边三角形ABC中,D是AB边上的动点,以CD为一边,向上作等边三角形EDC,连接AE,
(1)求证:△DBC≌△EAC
(2)如图1,令BC=8,AC与DE交于点O,当AE⊥CE时,求AO的长.
(3)如图2,当图中的点D运动到边BA的延长线上,所作△EDC仍为等边三角形,且有AC⊥CE时,试猜想线段AE与线段CD的位置关系?并说明理由.(自己在图中画出图形后解答)
【答案】(1)见解析;(2)2;(3)AE垂直平分线段CD,理由见解析
【解析】
(1)已知的条件有AC=BC,CE=CD,我们发现∠BCD和∠ACE都是60°减去一个∠ACD,因此两三角形全等的条件就都凑齐了(SAS).
(2)首先证明AE∥BC,解直角三角形求出AE,OA即可解决问题.
(3)同(1)(2)的思路完全相同,也是通过先证明三角形BCD和ACE全等,得出∠EAC=∠B=60°,又由∠ABC=∠ACB=60°,得出这两条线段之间的内错角相等,从而得出平行的结论.
解:(1)证明:如图1中,

∵∠ACB=60°,∠DCE=60°
∴∠BCD=60°﹣∠ACD,∠ACE=60°﹣∠ACD
∴∠BCD=∠ACE
在△DBC和△EAC中,
∵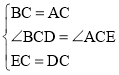 ,
,
∴△DBC≌△EAC(SAS),
解:(2)∵△DBC≌△EAC
∴∠EAC=∠B=60°
又∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC,
∵EC⊥AE,
∴∠AEC=90°,∠ACE=30°,
∴AE=![]() AC=4,
AC=4,
∴∠DEC=60°,
∴∠AEO=30°,
∵∠EAO=60°,
∴∠AOE=180°﹣∠AEO﹣∠EAO=90°,'
∴OA=![]() AE=2.
AE=2.
(3)结论:AE垂直平分线段CD.
理由:如图2中,设AE交CD于O.
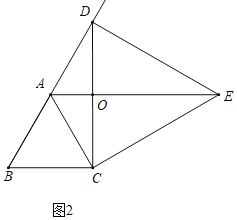
∵△ABC、△EDC为等边三角形
∴BC=AC,DC=CE,∠BCA=∠DCE=60°
∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE
在△DBC和△EAC中,
∵ ,
,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°
又∵∠ACB=60°
∴∠EAC=∠ACB=60°,
∵EC⊥AC,
∴∠ACE=90°,
∴∠AEC=90°﹣60°=30°,
∵∠DEC=60°,
∴∠DEO=∠CEO=30°,
∵ED=EC,
∴EA垂直平分线段CD.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案