题目内容
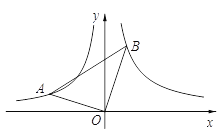
【题目】如图,∠ AOB=90°,且点A,B分别在反比例函数![]() (x<0),
(x<0),![]() (x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
(1)求k1,k2的值;
(2)连接AB,求tan∠ OBA的值.
【答案】(1)k1=-2,k2=3.
(2)tan∠OBA=![]() .
.
【解析】解:(1)∵k1,k2分别是方程x2-x-6=0的两根,∴解方程x2-x-6=0,得x1=3,x2=-2.结合图像可知:k1<0,k2>0,∴k1=-2,k2=3.
(2)如图,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.

由(1)知,点A,B分别在反比例函数![]() (x<0),
(x<0),![]() (x>0)的图象上,
(x>0)的图象上,
∴S△ACO=![]() ×
×![]() =1 ,S△ODB=
=1 ,S△ODB=![]() ×3=
×3=![]() .∵∠ AOB=90°,
.∵∠ AOB=90°,
∴∠ AOC+∠ BOD=90°,∵∠ AOC+∠ OAC=90°,∴∠ OAC=∠ BOD.
又∵∠ACO=∠ODB=90°,∴△ACO∽△ODB.
∴![]() =
=![]() =
=![]() ,∴
,∴![]() =±
=±![]() (舍负取正),即
(舍负取正),即![]() =
=![]() .
.
∴在Rt△AOB中,tan∠ OBA=![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目