题目内容
【题目】阅读理解
如图 a,在△ABC 中,D 是 BC 的中点.如果用 SABC 表示△ABC 的面积,则由等底等高的三角形的面积相等,可得![]()
![]()
![]()
![]() .同理,如图 b,在 ABC 中,D、E 是 BC 的三等分点,可得
.同理,如图 b,在 ABC 中,D、E 是 BC 的三等分点,可得![]()
![]()
![]()
![]()
![]()

结论应用
已知△ABC 的面积为 42,请利用上面的结论解决下列问题:


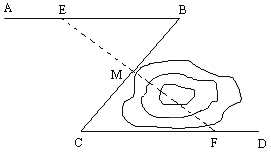
(1)如图 1,若 D、E 分别是 AB、AC 的中点,CD 与 BE交于点 F,则△DBF 的面积为 ;
类比推广
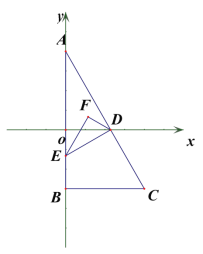
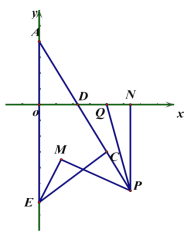
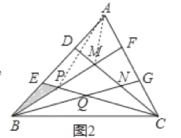
(2)如图 2,若 D、E 是 AB 的三等分点,F、G 是 AC 的 三等分点,CD 分别交 BF、BG 于 M、N,CE 分别交 BF、BG 于 P、Q,求△BEP 的面积;
(3)如图2,问题(2)中的条件不变,求四边形EPMD的面积.
【答案】(1)7;(2)2;(3)5.
【解析】
(1)根据中位线的性质得到△DOE∽△COB,再用相似三角形的性质,对应边的比等于相似比,![]() ,求得S
,求得S![]() :S
:S![]() =1:3,进而求得S
=1:3,进而求得S![]() :=
:=![]() S
S![]() ,即可求得;
,即可求得;
(2)连AP,AM,设S![]() =a,S
=a,S![]() =b,根据S
=b,根据S![]() =S
=S![]() =S
=S![]() =
=![]() S
S![]() .列出关于面积的方程组,解方程组即可求得;
.列出关于面积的方程组,解方程组即可求得;
(3)先求得四边形ADMF的面积,利用S![]() =S
=S![]() -S
-S![]() -S
-S![]() 即可求得;
即可求得;
(1)如图1,∵D,E分别是AB,AC的中点,
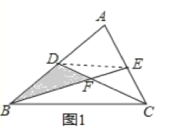
∴DE∥BC,DE=![]() BC.
BC.
∴△DOE∽△COB,△ADE∽△ABC,
∴![]() ,
,
∴S![]() :S
:S![]() =1:3,
=1:3,
∵S![]() =
=![]() S
S![]() ,
,
∴S![]() :=
:=![]() S
S![]() = S
= S![]() :=
:=![]() ×42=7,
×42=7,
(2)如图2,连AP,AM,设S![]() =a,S
=a,S![]() =b,
=b,
则S![]() =2a,S
=2a,S![]() =2b,
=2b,
则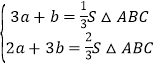 ,
,
即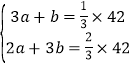 ,
,
解得![]() .
.
故△BEP的面积为2;
(3)设S![]() =x,S
=x,S![]() =y.
=y.
则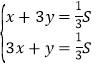 ,
,
即![]()
两式联立可得:x+y=7,
即S![]() =7;
=7;
S![]() =
=![]() S
S![]() =14,
=14,
故S![]() =S
=S![]() -S
-S![]() -S
-S![]() =142-7=5,
=142-7=5,

【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.