题目内容
【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=![]() .
.
(1)求AD和AB的长;
(2)求sin∠BAD的值.

【答案】(1)AB=5,AD=![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由中点定义求BC=4,根据tanB=![]() 得:AC=3,由勾股定理得:AB=5,AD=
得:AC=3,由勾股定理得:AB=5,AD=![]() ;
;
(2)作高线DE,证明△DEB∽△ACB,求DE的长,再利用三角函数定义求结果.
试题解析:(1)∵D是BC的中点,CD=2,
∴BD=DC=2,BC=4,
在Rt△ACB中,由tanB=![]() ,
,
∴![]() ,
,
∴AC=3,
由勾股定理得:AD=![]() ,
,
AB=![]() =5;
=5;
(2)过点D作DE⊥AB于E,

∴∠C=∠DEB=90°,
又∠B=∠B,
∴△DEB∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴DE=![]() ,
,
∴sin∠BAD=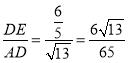 .
.

练习册系列答案
相关题目