题目内容
【题目】△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( ) 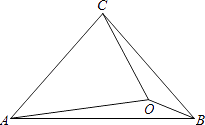
A.55°
B.60°
C.70°
D.80°
【答案】C
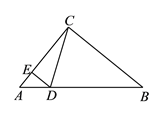
【解析】解:如图,作CD⊥AB于D,延长BO交CD于P,连接PA, 
∵∠CAB=∠CBA=50°,
∴AC=BC,
∴AD=BD,
∵∠CAB=∠CBA=50°,
∴∠ACB=80°,
∵∠ABC=∠ACB=50°,∠OBC=20°,
∴∠CBP=∠OBC=20°=∠CAP,
∠PAO=∠CAB﹣∠CAP﹣∠OAB=50°﹣20°﹣10°=20°=∠CAP,
∠POA=∠OBA+∠OAB=10°+50°﹣20°=40°=∠ACD,
∵在△CAP和△OAP中,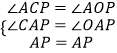 ,
,
∴△CAP≌△OAP,
∴AC=OA,
∴∠ACO=∠AOC,
∴∠OCA= ![]() (180°﹣∠CAO)=
(180°﹣∠CAO)= ![]() [180°﹣(∠CAB﹣∠OAB)=
[180°﹣(∠CAB﹣∠OAB)= ![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
故选:C.
【考点精析】关于本题考查的三角形的内角和外角,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目