Question

【题目】如图，在等边三角形ABC中，AB=6，点P是AB边上的任意一点（点P不与点A、点B重合），过点P作PD⊥AB，交直线BC于点D，作PE⊥AC，垂足为点F．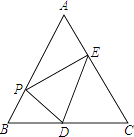

（1）求∠APE的度数；
（2）连接DE，当△PDE为等边三角形时，求BP的长．

Answer 1

【答案】
（1）解：∵△ABC为等边三角形，

∴∠A=∠B=∠C=60°，

∵PE⊥AC，

∴∠AEP=90°，

∴∠APE=180°﹣∠A﹣∠AEP=180°﹣60°﹣90°=30°

（2）解：设BP=x，则AP=6﹣x，

在Rt△BPD中，PD=BPtan60°= x，在Rt△APE中，PE=APsin60°= ，

∵△PDE为等边三角形，

∴PD=PE，

即 = （6﹣x），

解得：x=2，

∴当△PDE为等边三角形时，BP的长为2

【解析】（1）利用等边三角形的性质可得∠A=∠B=∠C=60°，在利用垂直的定义和三角形内角和定理可得结果；（2）设BP=x，根据等边三角形的性质，利用三角函数，易得PD= x，在Rt△APE中，PE=APsin60°= ，利用等边三角形的性质可得PE=PD，建立等量关系，解得x．