题目内容
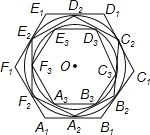
【题目】如图，正六边形A1B1C1D1E1F1的边长为2，正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切，正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切，…按这样的规律进行下去，A10B10C10D10E10F10的边长为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】解：连结OE1，OD1，OD2，如图所示，
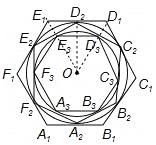
∵六边形A1B1C1D1E1F1为正六边形，
∴∠E1OD1=60°，
∴△E1OD1为等边三角形，
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切，
∴OD2⊥E1D1，
∴OD2=
E1D1=
×2，
∴正六边形A2B2C2D2E2F2的边长=
×2，
同理可得正六边形A3B3C3D3E3F3的边长=（
）2×2，
则正六边形A10B10C10D10E10F10的边长=（
）9×2=
．
故选D.
练习册系列答案
相关题目
