题目内容
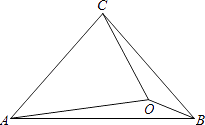
【题目】如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O. 
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
【答案】
(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS),
∴AB=DC
(2)解:△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形
【解析】(1)根据BE=CF得到BF=CE,又∠A=∠D,∠B=∠C,所以△ABF≌△DCE,根据全等三角形对应边相等即可得证;(2)根据三角形全等得∠AFB=∠DEC,所以是等腰三角形.
【考点精析】关于本题考查的等腰三角形的判定,需要了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能得出正确答案.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目