题目内容
【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | p | t | n | t | 0 | … |
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
由抛物线的对称性可求对称轴为:![]() ,可得p=0,即x=﹣1,x=3是方程ax2+bx+c=0的两个根,可判断②;当x=0,y=c=t>0,可得p+2t=0+2t>0,可判断③;由抛物线中在对称轴的右边,y随x的增大而减小,可得的a<0,由对称轴x=1可得b=﹣2a>0,可判断①;由x=3,y=0,可得c=﹣3a,由顶点坐标为(1,n),a<0,可得am2+bm+c≤a+b+c,可得am2+bm≤﹣4a﹣c,可判断④,即可求解.
,可得p=0,即x=﹣1,x=3是方程ax2+bx+c=0的两个根,可判断②;当x=0,y=c=t>0,可得p+2t=0+2t>0,可判断③;由抛物线中在对称轴的右边,y随x的增大而减小,可得的a<0,由对称轴x=1可得b=﹣2a>0,可判断①;由x=3,y=0,可得c=﹣3a,由顶点坐标为(1,n),a<0,可得am2+bm+c≤a+b+c,可得am2+bm≤﹣4a﹣c,可判断④,即可求解.
解:∵当x=0和x=2时,y=t,
∴对称轴为:![]() ,
,
∴当x=3和x=﹣1时,y的值相等,
∴p=0,
∴x=﹣1,x=3是方程ax2+bx+c=0的两个根,故②正确;
∵当x=0时,y=t,且c>0,
∴t=c>0,
∴p+2t=0+2t>0,故③错误;
∵x=2,y=t>0,x=3,y=0,
∴在对称轴的右边,y随x的增大而减小,
∴a<0,
∵x=![]() ,
,
∴b=﹣2a>0,故①正确;
∵当x=3时,y=0,
∴9a+3b+c=0,
∴3a+c=0,
∴c=﹣3a,
∴﹣4a﹣c=﹣4a+3a=﹣a,
∵顶点坐标为(1,n),a<0,
∴am2+bm+c≤a+b+c,
∴am2+bm≤a+b,
∴am2+bm≤﹣a,
∴am2+bm≤﹣4a﹣c,故④正确,
综上,共有3个结论正确,
故选:C.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】某校为提高学生体考成绩,对全校300名九年级学生进行一分种跳绳训练.为了解学生训练效果,学校体育组在九年级上学期开学初和学期末分别对九年级学生进行一分种跳绳测试,学生成绩均为整数,满分20分,大于18分为优秀.现随机抽取了同一部分学生的两次成绩进行整理、描述和分析.(成绩得分用x表示,共分成五组:A.x<13,B.13≤x<15,C.15≤x<17,D.17≤x<19,E.19≤x≤20)
开学初抽取学生的成绩在D组中的数据是:17,17,17,17,17,18,18.
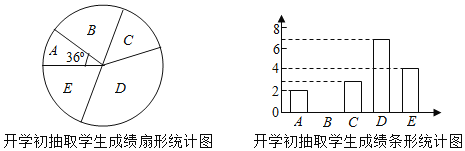
学期末抽取学生成绩统计表
学生成绩 | A组 | B组 | C组 | D组 | E组 |
人数 | 0 | 1 | 4 | 5 | a |
分析数据:
平均数 | 中位数 | 众数 | |
开学初抽取学生成绩 | 16 | b | 17 |
学期末抽取学生成绩 | 18 | 18.5 | 19 |
根据以上信息,解答下列问题:
(1)直接写出图表中a、b的值,并补全条形统计图;
(2)假设该校九年级学生都参加了两次测试,估计该校学期末成绩优秀的学生人数比开学初成绩优秀的学生人数增加了多少?
(3)小莉开学初测试成绩16分,学期末测试成绩19分,根据抽查的相关数据,请选择一个合适的统计量评价小莉的训练效果.