题目内容
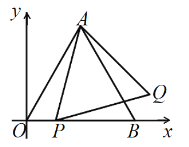
【题目】如图,平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是
是![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,以
,以![]() 为边长,在
为边长,在![]() 的右侧作等边
的右侧作等边![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() 与
与![]() 的函数关系式是________.
的函数关系式是________.
【答案】![]()
![]()
【解析】
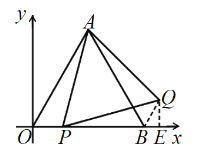
连接BQ,过点Q作QE⊥x轴于点E,先证明△AOP≌△ABQ,由此可得∠ABQ=60°,BQ=x,最后在Rt△QBE中,利用sin∠QBE=![]() 即可求得
即可求得![]() .
.
解:连接BQ,过点Q作QE⊥x轴于点E,则点Q的纵坐标为y=QE,
∵![]() ,
,![]() ,
,
∴△AOB为等边三角形,
∴AO=AB,∠OAB=∠ABO=60°,
∵△APQ为等边三角形,
∴AP=AQ,∠PAQ=60°,
∴∠PAQ=∠OAB,
∴∠OAP=∠BAQ,
在△AOP与△ABQ中,
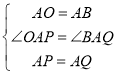
∴△AOP≌△ABQ(SAS),
∴∠ABQ=∠AOP=60°,BQ=OP=x,
∴∠QBE=180°-∠ABQ-∠ABO=60°,
∵QE⊥x轴,
∴∠QEB=90°,
∴在Rt△QBE中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() (x>0).
(x>0).

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | p | t | n | t | 0 | … |
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
A.1B.2C.3D.4