题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .

【答案】(2,4)或(8,4).
【解析】
试题分析:∵A(10,0),C(0,4),∴OA=10,OC=4,
∵点D是OA的中点,∴OD=![]() OA=5,
OA=5,
过点P作PE⊥x轴于E,
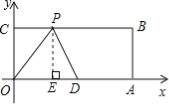
则PE=OC=4,
∵P(3,4),
∴OP=5,
∴此时,OP=OD,
∴DE=3,
若点E在点D的左边,OE=5﹣3=2,
此时,点P的坐标为(2,4),
若点E在点D的右边,则OE=5+3=8,
此时,点P的组别为(8,4),
综上所述,其余的点P的坐标为(2,4)或(8,4).
故答案是(2,4)或(8,4).

练习册系列答案
相关题目