题目内容
【题目】有如图所示的一块地,已知AD=4米,CD=3米,![]() ,AB=13米,BC=12米.
,AB=13米,BC=12米.
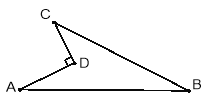
(1)试判断以点A、点B、点C为顶点的三角形是什么三角形?并说明理由.
(2)求这块地的面积.
【答案】(1)以点A、点B、点C为顶点的三角形是直角三角形;
(2)这块地的面积24m2.
【解析】
试题分析:根据勾股定理求得AC的长,再根据勾股定理的逆定理判定△ABC为直角三角形,从而不难求得这块地的面积.
试题解析:(1)以点A、点B、点C为顶点的三角形是直角三角形,理由是:
连接AC.

∵AD=4m,CD=3m,AD⊥DC
∴AC=5m
∵122+52=132
∴△ACB为直角三角形;
(2)∵△ACB为直角三角形
∴S△ACB=![]() ×AC×BC=
×AC×BC=![]() ×5×12=30m2,
×5×12=30m2,
S△ACD=![]() ADCD=
ADCD=![]() ×4×3=6m2,
×4×3=6m2,
∴这块地的面积=S△ACB﹣S△ACD=30﹣6=24m2.

练习册系列答案
相关题目
【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%