题目内容
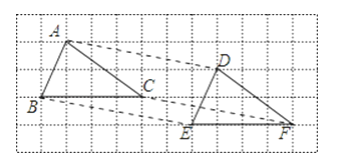
【题目】(1)阅读并回答:科学实验证明,平面镜反射的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2, ∠3=∠4.
①由条件可知:∠1与∠3的大小关系是_____,∠2与∠4的大小关系是________;
②反射光线BC与EF的位置关系是___________,理由是___________;
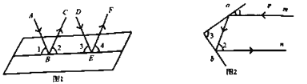
(2)解决问题:①如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=35°,则∠2=_______,∠3=_______;
②在①中,若∠1=40°,则∠3=_______,
③由①②请你猜想:当∠3=_______时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
【答案】(1)①相等;相等②平行,理由是同位角相等,两直线平行;(2)①∠2=70°70°,∠3=90°;②∠3=90°;③猜想:当∠3=90°时,m总平行于n,理由见解析.
【解析】
(1)根据平行线的判定与性质逐一求解可得;
(2)①根据入射角等于反射角得出∠1=∠4,∠5=∠7,求出∠6,根据平行线性质即可求出∠2,求出∠5,根据三角形内角和求出∠3即可;
②与①同理;
③求出∠4+∠5,求出∠1+∠4+∠5+∠7,即可求出∠2+∠6,根据平行线的判定推出即可.
解:(1)①由条件可知:∠1与∠3的大小关系是相等,理由是两直线平行,同位角相等;∠2与∠4的大小关系是相等;
②反射光线BC与EF的位置关系是平行,理由是同位角相等,两直线平行;
故答案为:①相等、两直线平行,同位角相等、相等;②平行、同位角相等,两直线平行.
(2)①如图,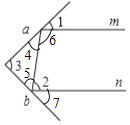
∵∠1=35°,
∴∠4=∠1=35°,
∴∠6=180°-35°-35°=110°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=70°,
∴∠5=∠7=55°,
∴∠3=180°-55°-35°=90°;
②在①中,若∠1=40°,则∠4=∠1=40°,
∴∠6=180°-40°-40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7=50°,
∴∠3=180°-50°-40°=90°
③猜想:当∠3=90°时,m总平行于n,
理由:∵三角形的内角和为180°,又∠3=90°,
∴∠4+∠5=90°
∵∠4=∠1、∠5=∠7,
∴∠1+∠7=90°,
∴∠1+∠4+∠5+∠7=90°+90°=180°,
∵∠1+∠4+∠6+∠5+∠2+∠7=180°+180°=360°,
∴∠6+∠2=180°
∴m∥n(同旁内角互补,而直线平行)
故答案为:①70°、90°;②90°;③90°.

【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…
(1)观察图形并完成表格:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图n中,菱形的个数为 [用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .