题目内容
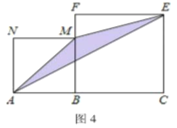
【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴∠FAB=∠ABE=90°,AF∥BE,
∵EF⊥AD,
∴∠FAB=∠ABE=∠AFE=90°,
∴四边形ABEF是矩形,
∵AE平分∠BAD,AF∥BE,
∴∠FAE=∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是正方形;
(2)解:过点P作PH⊥AD于H,如图所示:

∵四边形ABEF是正方形,
∴BP=PF,BA⊥AD,∠PAF=45°,
∴AB∥PH,
∵AB=6,
∴AH=PH=3,
∵AD=8,
∴DH=AD﹣AH=8﹣3=5,
在Rt△PHD中,∠PHD=90°.
∴tan∠ADP= ![]() =
= ![]() .
.
【解析】(1)先根据有一角为直角的平行四边形是矩形证四边形ABEF是矩形,然后再证AB=BE,可得证;
(2)过点P作PH⊥AD于H,根据四边形ABEF是正方形和已知,易求出DH、PH的长,再在在Rt△PHD中,利用三角函数的定义可求得答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…
(1)观察图形并完成表格:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图n中,菱形的个数为 [用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .