题目内容
如图所示,已知矩形ABCD中,AD=8cm,AB=6cm,对角线AC的垂直平分线交AD于E,交BC于F.

(1)试判断四边形AFCE是怎样的四边形;
(2)求出四边形AFCE的周长.

(1)试判断四边形AFCE是怎样的四边形;
(2)求出四边形AFCE的周长.
(1)菱形;(2)25cm
试题分析:(1)根据矩形的性质结合EF垂直平分AC,可证得△AOE≌△COF,从而得到四边形AFCE为平行四边形,再有FE⊥AC,即可证得结论;
(2)设AE=xcm,根据矩形、菱形的性质结合勾股定理即可列方程求解.
(1)∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
又∠AOE=∠COF,
∴△AOE≌△COF,
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AFCE为菱形;
(2)∵四边形ABCD是矩形,
∴AB=CD=6cm,∠D=90°
∵四边形AFCE为菱形,
∴AE=CE
设AE=CE =xcm,则DE=(8-x)cm
在Rt△CDE中,
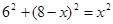
解得
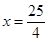
则四边形AFCE的周长

点评:解答本题的关键是熟练掌握矩形的对边平行且相等,四个角都为直角;对角线互相垂直的平行四边形为菱形.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
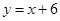 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.
 有3个有效数字;
有3个有效数字; 、
、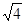 、
、 为边长能组成一个直角三角形
为边长能组成一个直角三角形 的对角线
的对角线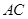 和
和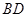 相交于点
相交于点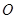 ,过点
,过点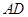 和
和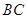 于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
于点E、F,AB=2,BC=4,则图中阴影部分的面积为 . 


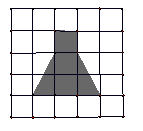
 ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )
ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )