题目内容
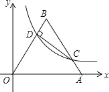
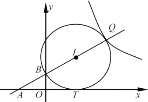
【题目】如图,在平面直角坐标系中,直线l:y=kx+1(k>0)与x轴、y轴分别相交于点A、B,tan∠ABO=![]() .
.
(1)求k的值;
(2)若直线l:y=kx+1与双曲线y=![]() (
(![]() )的一个交点Q在一象限内,以BQ为直径的⊙I与x轴相明于点T,求m的值.
)的一个交点Q在一象限内,以BQ为直径的⊙I与x轴相明于点T,求m的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)在![]() 中,令
中,令![]() , 求得
, 求得![]() ,在
,在![]() 中,利用
中,利用
![]() 求得
求得![]() ,故
,故![]() .,把点
.,把点![]() 代入
代入![]() 中求得
中求得![]() ;
;
(2) 连接![]() ,由⊙
,由⊙![]() 与
与![]() 轴相切于点
轴相切于点![]() ,得
,得![]() ,在
,在![]() 中,
中,![]() ,求得
,求得
![]() , 在
, 在![]() 中,
中,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() , 作
, 作![]() 轴于点
轴于点![]() ,在
,在![]() 中,
中,![]() ,求得
,求得![]() ,
, ![]() ,得出
,得出![]() , 可得
, 可得![]() ,把点
,把点![]() 代入
代入![]() 即可求出m的值
即可求出m的值
解:
(1)在![]() 中,令
中,令![]() ,则
,则![]() ,
,
∴![]()
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() .
.
把点![]() 代入
代入![]() 中得:
中得:![]() ,
,
解得:![]()
(2)∵![]() ,∴
,∴![]() ,
,![]()
连接![]() ,∵⊙
,∵⊙![]() 与
与![]() 轴相切于点
轴相切于点![]() ,∴
,∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() ,
,
作![]() 轴于点
轴于点![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
把点![]() 代入
代入![]() 得:
得:![]() .
.

练习册系列答案
相关题目