��Ŀ����
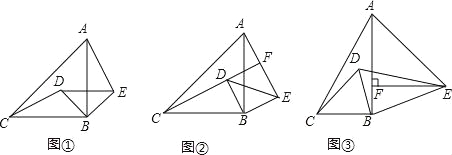
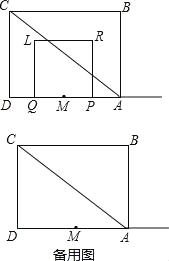
����Ŀ����ͼ���ı���ABCDΪ���Σ�ACΪ�Խ��ߣ�AB=6��BC=8����M��AD���е㣬P��Q����ͬʱ�ӵ�M��������P������MA�����˶�����Q���߶�MD�������˶�����D���������˶�����Mֹͣ����P��ֹ֮ͣ�˶���P��Q�����˶����ٶȾ�Ϊÿ��1����λ����PQΪһ��������������PRLQ�����P���˶�ʱ��Ϊt���룩��������PRLQ����ABC�ص����ֵ����ΪS��
��1������R���߶�AC��ʱ�����t��ֵ��
��2�����S��t֮��ĺ�����ϵʽ����ֱ��д��ȡֵ��Χ����������ϵʽʱ��ֻ��д���ص�����Ϊ������ʱ����ϸ���̣��������ֱ��д��������ϵʽ����
��3���ڵ�P����Q�˶���ͬʱ����һ��E��ÿ��1����λ���ٶȴ�C��B�˶�����tΪ��ֵʱ����LRE�ǵ��������Σ���ֱ��д��t��ֵ��ȡֵ��Χ��
���𰸡���1��t=![]() ��
��
��2��S��t֮��ĺ�����ϵʽΪ��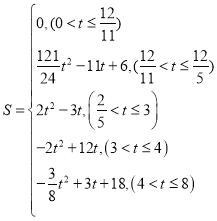 ��
��
��3��t��ȡֵ��Χ��4��t��8ʱ����LRE�ǵ��������Σ���t=4s����t=8s��![]() s��
s��![]() sʱ����LRE�ǵ��������Σ�
sʱ����LRE�ǵ��������Σ�
��������
�����������1���������������ƿɵ�![]() ����
����![]() ����ɣ�
����ɣ�
��2�����ݵ�P�͵�Q���˶������������۽�ɣ�
��3��������LRE�ǵ��������������������
�����������1������R���߶�AC��ʱ��Ӧ�����㣺![]() ��
��
��MPΪt����PR=2t��AP=4��t��
���ɵã�![]() ����
����![]() ��
��
��ã�t=![]() ��
��
��2����![]() ʱ��������PRLQ����ABCû���ص����֣������ص����ֵ����Ϊ0��
ʱ��������PRLQ����ABCû���ص����֣������ص����ֵ����Ϊ0��
��![]() ʱ��������PRLQ����ABC�ص����ֵ����Ϊֱ��������KRW�����=
ʱ��������PRLQ����ABC�ص����ֵ����Ϊֱ��������KRW�����=![]() ��
��
![]() ��
��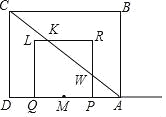
��![]() ʱ��������PRLQ����ABC�ص����ֵ����=
ʱ��������PRLQ����ABC�ص����ֵ����=![]() ����2t��3��2t=2t2��3t��
����2t��3��2t=2t2��3t��
��3��t��4ʱ��������PRLQ����ABC�ص����ֵ����=![]() ����12��2t����2t=��2t2+12t��
����12��2t����2t=��2t2+12t��
��4��t��8ʱ��������PRLQ����ABC�ص����ֵ����ΪS=![]() ��
��
��������S��t֮��ĺ�����ϵʽΪ��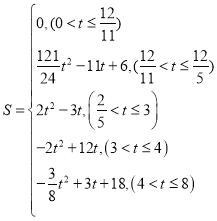 ��
��
��3���ڵ�P����Q�˶���ͬʱ����һ��E��ÿ��1����λ���ٶȴ�C��B�˶���
�ٵ���E��BC���е�ʱ����E��LR���д�������ʱ��EL=ER����ʱt=4s����LRE�ǵ��������Σ�
����E���B�غ�ʱ����E��LR���д�������ʱ��EL=ER����ʱt=8s����LRE�ǵ��������Σ�
����������t��ȡֵ��Χ��4��t��8��
�ڵ�EL=LRʱ����ͼ��ʾ��

LR=2t��CF=NL=4��t����EF=2t��4��FL=CN=6��2t��
����ֱ����EFL�У��ɹ��ɶ����õ���EL2=EF2+FL2=��2t��4��2+��6��2t��2��
����EL=LR�õ���EL2=LR2����4t2=10t2��40t+52��
��������
t2��10t+13=0��
��� t1=5+2![]() ����ȥ����t2=5��2
����ȥ����t2=5��2![]() ��
��
���Ե�t=5��2![]() ��s��ʱ����LRE�ǵ��������Σ�
��s��ʱ����LRE�ǵ��������Σ�
ͬ������ER=LRʱ��![]() ��
��
����������t��ȡֵ��Χ��4��t��8ʱ����LRE�ǵ��������Σ���t=4s����t=8s��![]() s��
s��![]() sʱ����LRE�ǵ��������Σ�
sʱ����LRE�ǵ��������Σ�
����;�ı����ۺ��⣮