Question

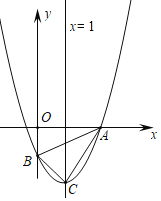
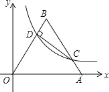
【题目】如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线y＝上（k＞0，x＞0），则k的值为（　　）

A. 25B. 18 C. 9D. 9

Answer 1

【答案】D

【解析】

根据等边三角形的性质表示出D，C点坐标，进而利用反比例函数图象上点的坐标特征得出答案．

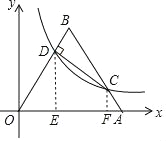
解：过点D作DE⊥x轴于点E，过C作CF⊥x轴于点F，如图所示．

可得：∠ODE＝30∠BCD＝30°，

设OE＝a，则OD＝2a，DE＝ a，

∴BD＝OB﹣OD＝10﹣2a，BC＝2BD＝20﹣4a，AC＝AB﹣BC＝4a﹣10，

∴AF＝AC＝2a﹣5，CF＝ AF＝（2a﹣5），OF＝OA﹣AF＝15﹣2a，

∴点D（a， a），点C[15﹣2a，（2a﹣5）]．

∵点C、D都在双曲线y＝上（k＞0，x＞0），

∴a a＝（15﹣2a）×（2a﹣5），

解得：a＝3或a＝5．

当a＝5时，DO＝OB，AC＝AB，点C、D与点B重合，不符合题意，

∴a＝5舍去．

∴点D（3，3），

∴k＝3×3＝9．

故选：D．