题目内容
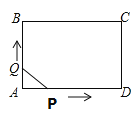
【题目】已知:如图,矩形ABCD中,AB=2cm,AD=3cm.点P和点Q同时从点A出发,点P以3cm/s的速度沿A→D方向运动到点D为止,点Q以2cm/s的速度沿A→B→C→D方向运动到点D为止,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )
A.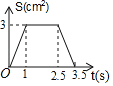 B.
B.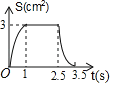
C.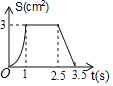 D.
D.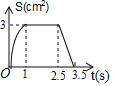
【答案】C
【解析】
研究两个动点到矩形各顶点时的时间,分段讨论求出函数解析式即可求解.
解:分三种情况讨论:
(1)当0≤t≤1时,点P在AD边上,点Q在AB边上,
∴S=![]() ,
,
∴此时抛物线经过坐标原点并且开口向上;
(2)当1<t≤2.5时,点P与点D重合,点Q在BC边上,
∴S=![]() =3,
=3,
∴此时,函数值不变,函数图象为平行于t轴的线段;
(3)当2.5<t≤3.5时,点P与点D重合,点Q在CD边上,
∴S=![]() ×3×(7﹣2t))=﹣t+
×3×(7﹣2t))=﹣t+![]() .
.
∴函数图象是一条线段且S随t的增大而减小.
故选:C.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目