题目内容
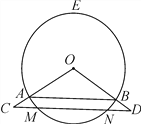
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3![]() -3,CD∥AB,并与弧AB相交于点M、N.
-3,CD∥AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若sin∠C=![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
【答案】(1)线段OD的长为![]() ;
;
(2)弦MN的长为3;
(3)优弧MEN的长度![]() .
.
【解析】分析:(1)由OA=OB得:OA=OB,根据CD∥AB可知,∠OAB=∠C, ∠D=∠OBA,推出∠C=∠D,最后求出OD的长;(2)过O作OF⊥CD,连接OM,由垂径定理可知MF=![]() MN,再根据sin∠C=
MN,再根据sin∠C=![]() 可求出OF的长,利用勾股定理即可求出ME的长,进而求出答案.(3)由OM=ON=MN得到△OMN是等边三角形,利用弧长公式求解.
可求出OF的长,利用勾股定理即可求出ME的长,进而求出答案.(3)由OM=ON=MN得到△OMN是等边三角形,利用弧长公式求解.
本题解析:(1)∵OA=OB ∴OA=OB
∵CD∥AB ∴∠OAB=∠C, ∠D=∠OBA
∴∠C=∠D ∴OD=OC=OA+AC=![]()
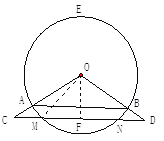 (2)过O作OF⊥MN于点F,连结OM。
(2)过O作OF⊥MN于点F,连结OM。
∵![]() ,OC=
,OC=![]() ∴OF=
∴OF=![]() ∵OM=3 根据勾股定理得MF=
∵OM=3 根据勾股定理得MF=![]()
由垂径定理得MN=3, (3)由(2)可得△OMN是等边三角形,∴∠MON=60°
∴优弧MEN的长度=![]()

练习册系列答案
相关题目