题目内容
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E,F.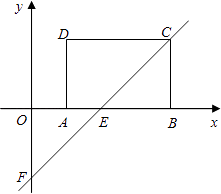
(1)求矩形ABCD的顶点A,B,C,D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x﹣2上一点,若S△POE=5,求点P的坐标.
【答案】
(1)
解:∵AD=BC=2,
故可设点C的坐标为(m,2),
又∵点C在直线y=x﹣2上,
∴2=m﹣2,
解得:m=4,即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
故可得点A,B,D的坐标分别为(1,0)、(4,0)、(1,2)
(2)
解:直线y=x﹣2与x轴、y轴坐标分别为E (2,0)、F (0,﹣2),
∴OF=OE=BC=BE=2,
在RT△OEF和RT△BEC中, 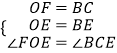
故可得△OEF≌△BEC
(3)
解:设点P的坐标为(xp,yp),则S△POE= ![]() ×OE×|yp|=
×OE×|yp|= ![]() ×2×|yp|=5,
×2×|yp|=5,
解得:yp=±5,
①当yp=5时,xp=7;②当yp=﹣5时,xp=﹣3,
故点P的坐标为(7,5)或(﹣3,﹣5)
【解析】(1)根据题意可得点C的纵坐标为2,代入函数解析式可得出点C的坐标,结合矩形的性质可得出A、B、D的坐标;(2)先求出OE、OF的长度,从而利用SAS证明△OEF≌△BEC即可.(3)设点P的坐标为(xp , yp),则可表示出S△POE= ![]() ×OE×|yp|,解出xp的值讨论即可.
×OE×|yp|,解出xp的值讨论即可.

练习册系列答案
相关题目