题目内容
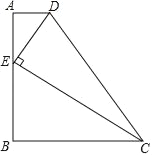
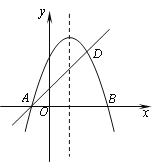
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧![]() 的中点BD交AC于点E.
的中点BD交AC于点E.
(1)求证:AD2=DEDB.
(2)若BC=5,CD=![]() ,求DE的长.
,求DE的长.

【答案】(1)详见解析;(2)DE=![]() .
.
【解析】
(1)根据D是劣弧![]() 的中点,有∠DAC=∠ABD,结合公共角∠ADB,证明△ABD∽△EAD列出比例式即可;
的中点,有∠DAC=∠ABD,结合公共角∠ADB,证明△ABD∽△EAD列出比例式即可;
(2)根据D是劣弧![]() 的中点,有AD=CD,故DC2=DEDB,然后由BC是直径,可得△BCD是直角三角形,利用勾股定理求出BD的长即可解决问题.
的中点,有AD=CD,故DC2=DEDB,然后由BC是直径,可得△BCD是直角三角形,利用勾股定理求出BD的长即可解决问题.
(1)证明:∵D是劣弧![]() 的中点,
的中点,
∴![]() ,
,
∴∠ABD=∠DAC,
又∵∠ADB=∠EDA,
∴△ABD∽△EAD,
∴![]() =
=![]() ,
,
∴AD2=DEDB;
(2)解:由D是劣弧![]() 的中点,得AD=DC,则DC2=DEDB,
的中点,得AD=DC,则DC2=DEDB,
∵BC是直径,
∴△BCD是直角三角形,
∴BD=![]() =
=![]() =2
=2![]() ,
,
由DC2=DEDB得:(![]() )2=2
)2=2![]() DE,
DE,
解得:DE=![]() .
.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目