题目内容
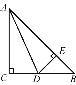
【题目】如图,在ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF=.
【答案】![]()
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE:BE=4:3,
∴BE:AB=3:7,
∴BE:CD=3:7.
∵AB∥CD,
∴△BEF∽△DCF,
∴BF:DF=BE:CD=3:7,
即2:DF=3:7,
∴DF= ![]() .
.
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.

练习册系列答案
相关题目
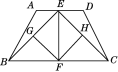
【题目】有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如图).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的倍.
【题目】某商店甲、乙两种商品三天销售情况的账目记录如下表:
日期 | 卖出甲商品的数量(个) | 卖出乙商品的数量(个) | 收入(元) |
第一天 | 39 | 21 | 321 |
第二天 | 26 | 14 | 204 |
第三天 | 39 | 25 | 345 |
(1)财务主管在核查时发现:第一天的账目正确,但其他两天的账目有一天有误,请你判断第几天的账目有误,并说明理由;
(2)求甲、乙两种商品的单价.