题目内容
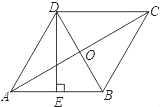
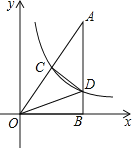
【题目】如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=![]() 经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .
经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .
【答案】6
【解析】
试题分析:过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=![]() |k|.
|k|.
解:如图,过C点作CE⊥x轴,垂足为E.
∵Rt△OAB中,∠OBA=90°,
∴CE∥AB,
∵C为Rt△OAB斜边OA的中点C,
∴CE为Rt△OAB的中位线,
∵△OEC∽△OBA,
∴![]() =
=![]() .
.
∵双曲线的解析式是y=![]() ,即xy=k
,即xy=k
∴S△BOD=S△COE=![]() |k|,
|k|,
∴S△AOB=4S△COE=2|k|,
由S△AOB﹣S△BOD=S△AOD=2S△DOC=18,得2k﹣![]() k=18,
k=18,
k=12,
S△BOD=S△COE=![]() k=6,
k=6,
故答案为:6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目