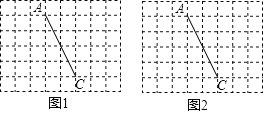Question

【题目】定义：一组邻边相等且对角互补的四边形叫做“邻等对补四边形”

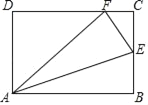
如图1，四边形ABCD中，AB＝BC，∠B+∠D＝180°（或∠A+∠C＝180°），则四边形ABCD叫做“邻等对补四边形”．

概念理解

（1）在以下四种图形中：①平行四边形，②菱形，③矩形，④正方形；一定是“邻等对补四边形”的是　 　；（填写序号）

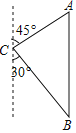
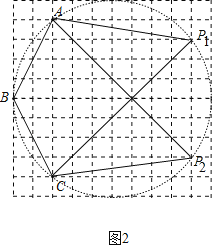
（2）如图2，点A、B、C是网格中格点，请找出两个格点P1，P2，连接P1A、P1C，P2A、P2C画出四边形P1ABC，P2ABC，使四边形P1ABC，P2ABC均为“邻等对补四边形”．

性质证明

（3）如图1，四边形ABCD中，AB＝BC，∠A+∠C＝180°，连接BD，求证：BD平分∠ADC．

知识运用

（4）如图3，在“邻等对补四边形”ABCD中，满足AB＝AD，AB+BC＝6，∠ADC＝60°时，若2≤BC＜3，求四边形ABCD的面积的最大值．

Answer 1

【答案】（1）④；（2）详见解析；（3）详见解析；（4）四边形ABCD的面积的最大值最大值为8．

【解析】

（1）根据“邻等对补四边形”的定义即可判断；（2）如图作△ABC的外接圆，图中点P1，P2即为所求（答案不唯一，在直线AC的右侧圆上的格点，即可满足条件）；（3）如图1中，连接AC，BD．证明A，B，C，D四点共圆，利用圆周角定理即可解决问题；（4）如图3中，延长CB到H，使得BH＝BA，连接AH，AC，作CE⊥AD于E，CF⊥AH于F，作AK⊥BH于K．设BC＝x．构建二次函数，利用二次函数的性质即可解决问题．

（1）根据“邻等对补四边形”的定义，正方形一定是“邻等对补四边形”．

故答案为：④．

（2）如图2中，作△ABC的外接圆，图中点P1，P2即为所求（答案不唯一）

（3）如图1中，连接AC，BD．

∵∠BAD+∠BCD＝180°，

∴A，B，C，D四点共圆，

∴BA＝BC，

∴，

∴∠ADB＝∠BDC，

∴BD平分∠ADC．

（4）如图3中，延长CB到H，使得BH＝BA，连接AH，AC，作CE⊥AD于E，CF⊥AH于F，作AK⊥BH于K．设BC＝x．

∵∠ADC+∠ABC＝180°，∠ADC＝60°，

∴∠ABC＝120°，

∴∠ABH＝60°，

∵BA＝BH，

∴△ABH是等边三角形，

∴∠H＝60°，

∴∠H＝∠D，

由（2）可知．AC平分∠BCD，

∴∠ACH＝∠ACD，

∵AC＝AC，

∴△ACH≌△ACD，

∴∠CAD＝∠CAH，

∵CE⊥AD，CF⊥AH，

∴CE＝CF，

∵BH+BC＝AB+BC＝6，

∴CF＝CE＝CHsin60°＝3，AK＝HKtan60°＝（6﹣x），

∴S四边形ABCD＝S△ADC+S△ACB＝（6﹣x）3+x（6﹣x）＝﹣x2+9，

∵2≤x＜3，

∴x＝2时，S有最大值，最大值S＝8，