题目内容
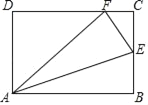
【题目】如图所示,将矩形ABCD沿AE折叠得到△AFE,且点B恰好与DC上的点F重合.
(1)求证:△ADF∽△FCE;
(2)若tan∠CEF=2,求tan∠AEB的值.
【答案】(1)见解析;(2)tan∠AEB=![]() .
.
【解析】
(1)因为△AEF是由△AEB翻折得到,推出∠AFB=∠B=90°,推出∠AFD+∠EFC=90°,∠EFC+∠FEC=90°,推出∠AFD=∠FEC,由此即可证明.
(2))由tan∠FEC![]() 2,推出CF=2EC,设EC=a,则FC=2a,EF=EB
2,推出CF=2EC,设EC=a,则FC=2a,EF=EB![]() a,由△ADF∽△FCE,得
a,由△ADF∽△FCE,得![]() ,即
,即![]() ,推出DF
,推出DF![]() a,根据tan∠AEB
a,根据tan∠AEB![]() 计算即可.
计算即可.
(1)∵四边形ABCD是矩形,∴AB=DC,AD=BC,∠D=∠C=∠B=90°.
∵△AEF是由△AEB翻折得到,∴∠AFB=∠B=90°,∴∠AFD+∠EFC=90°,∠EFC+∠FEC=90°,∴∠AFD=∠FEC.
∵∠D=∠C,∴△ADF∽△FCE.
(2)∵tan∠FEC![]() 2,∴CF=2EC,设EC=a,则FC=2a,EF=EB
2,∴CF=2EC,设EC=a,则FC=2a,EF=EB![]() a.
a.
∵△ADF∽△FCE,∴![]() ,∴
,∴![]() ,∴DF
,∴DF![]() a,∴AB=CD=DF+CF
a,∴AB=CD=DF+CF![]() a,∴tan∠AEB
a,∴tan∠AEB![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目